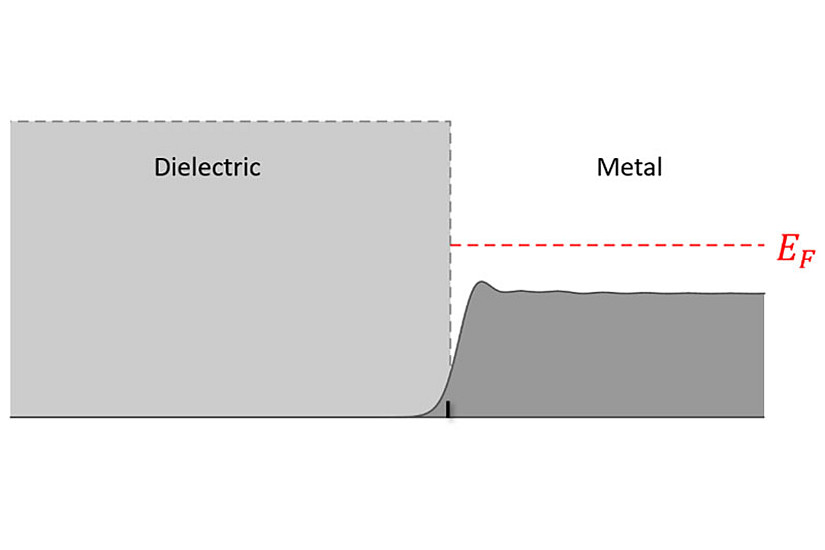
Maxwell’s equations belong to the cultural heritage of physics, the number of different phenomena they can describe is truly impressive. Even the interaction between light and matter can be elegantly accounted for through coarse graining and a few material parameters, which can be extracted from either experiment or quantum mechanical calculations. Only for Maxwell’s boundary conditions things occasionally turn out to be slightly involved, at the very boundary where the quantum mechanical wavefunction of the optically excited electrons leaks out of the material.
In the 1970s Peter Feibelman suggested to account for quantum mechanical modifications at planar boundaries through two frequency dependent parameters, which are nowadays named after him. The approach has been recently generalized by Yang et al., Nature 576, 248 (2019), for arbitrary boundaries, where the Feibelman parameters become part of modified, mesoscopic boundary conditions. However, the implementation of these boundary conditions into commercial Maxwell solvers turns out to be somewhat intricate.
In a paper that has just been accepted for publication in Physical Review B, Ulrich Hohenester and Gerhard Unger show how to implement mesoscopic boundary conditions elegantly and without too much effort into a boundary element method approach for the solution of Maxwell’s equations. Textbooks on electrodynamics will not have to be rewritten in the light of these results, mesoscopic boundary conditions remain a boundary effect. There (namely at the boundary), however, it now becomes possible to consider a wealth of quantum mechanical effects, which have gained increasing importance in the last couple of years for nanophotonic structures.
Ulrich Hohenester and Gerhard Unger, Nanoscale electromagnetism with the boundary element method, to appear in Phys. Rev. B (2022), https://link.aps.org/doi/10.1103/PhysRevB.105.075428